Resumen tema 4 Fracciones (6º)

Esquema-resumen de la unidad didáctica de las fracciones es el siguiente.

Fuente: editorial SM

Tema 4 fracciones (6º)

FRACCIONES.

1.-Fracciones.

Concepto:
Una fracción representa las partes que tomamos de una unidad dividida en partes iguales.
Términos. 
El denominador indica las partes en que dividimos la unidad y el numerador indica las partes que tomamos.

1.1.-Fracción de una cantidad: Para calcular la fracción de una cantidad, dividimos la cantidad entre el denominador y multiplicamos el resultado por el numerador.

1.2.-Tipos de fracciones:

-Las fracciones con el numerador menor que el denominador se llaman fracciones propias.

-Fracciones impropias:

Si el numerador es mayor que el denominador son fracciones impropias.

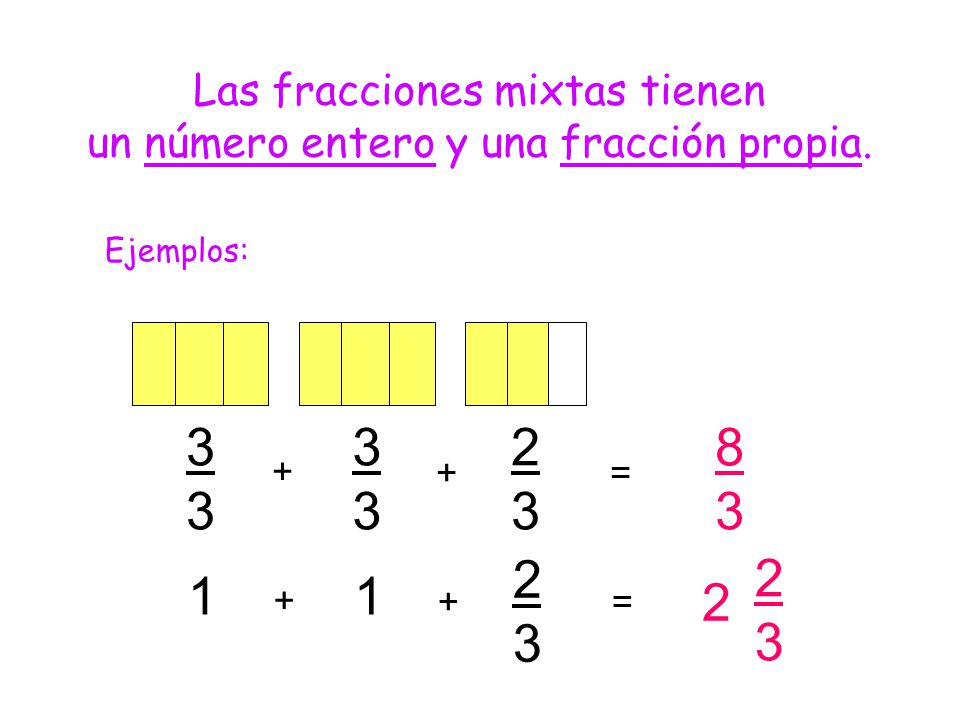
-Fracciones mixtas:

Están compuestas por un nº entero y una fracción propia.

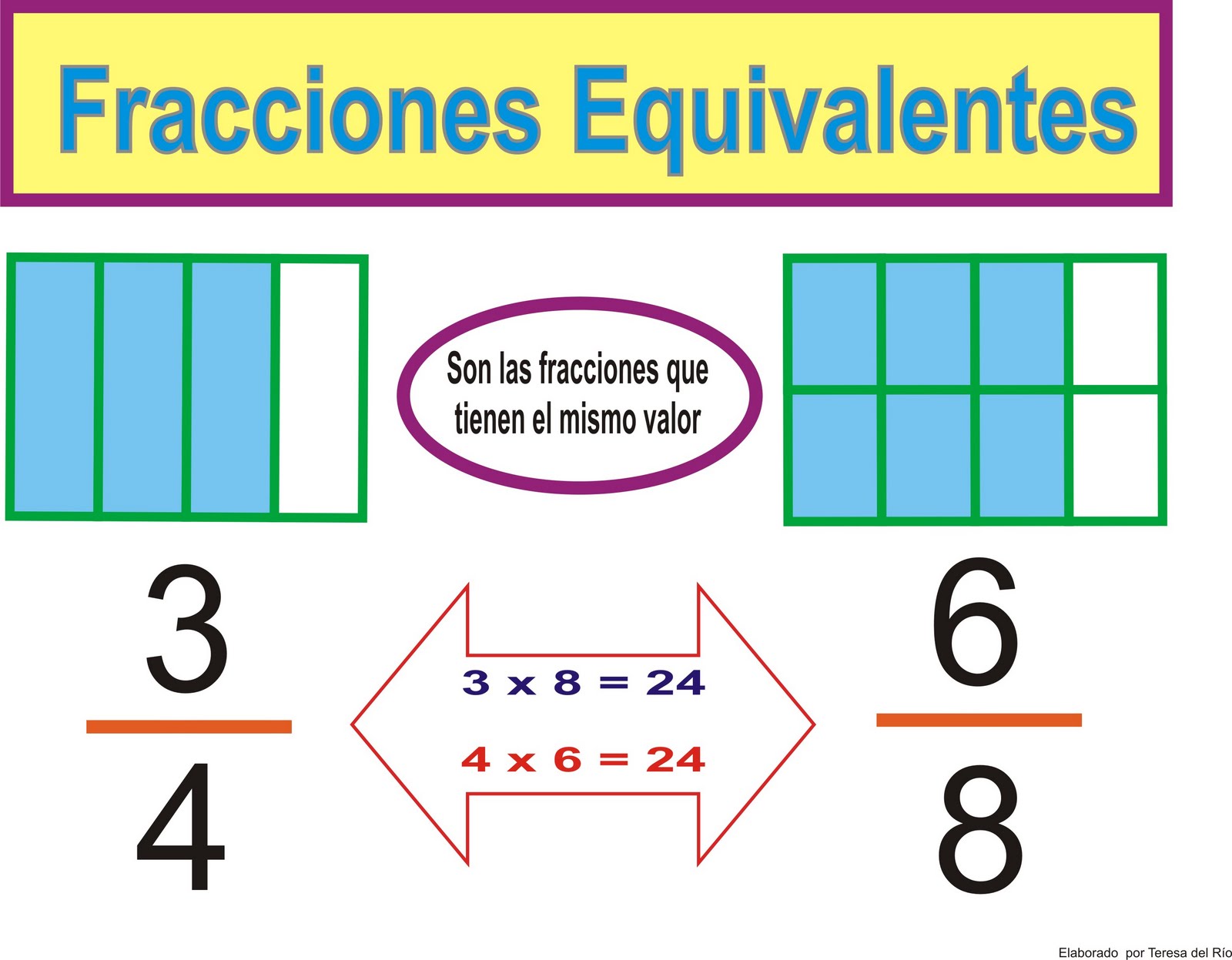
2.-Fracciones equivalentes.

• Dos fracciones equivalentes representan la misma cantidad.
• Si multiplicamos numerador y denominador por el mismo número obtenemos la fracción amplificada. Cuando los dividimos por el mismo número obtenemos la fracción simplificada.
• La fracción irreducible es la que no se puede simplificar más.

(Para hallar la fracción irreducible podemos dividir el numerador y el denominador por su máximo común divisor).

3.Reducir a común denominador: Comparar fracciones.

Para comparar fracciones con distinto numerador y denominador, las reducimos a común denominador. El denominador común es el mínimo común múltiplo de los denominadores (m.c.m.)

Cuando dos fracciones tienen el mismo denominador, es mayor la que tiene mayor numerador.

4.-Operaciones con fracciones: 

4.1.-Sumar y restar.

Muy importante:Para sumar o restar fracciones reducimos a común denominador. Después, sumamos o restamos los numeradores y escribimos el denominador común.

5.-Multiplicar fracciones:

Al multiplicar dos fracciones se obtiene otra fracción en la que el numerador es el producto de los numeradores y el denominador es el producto de los denominadores.

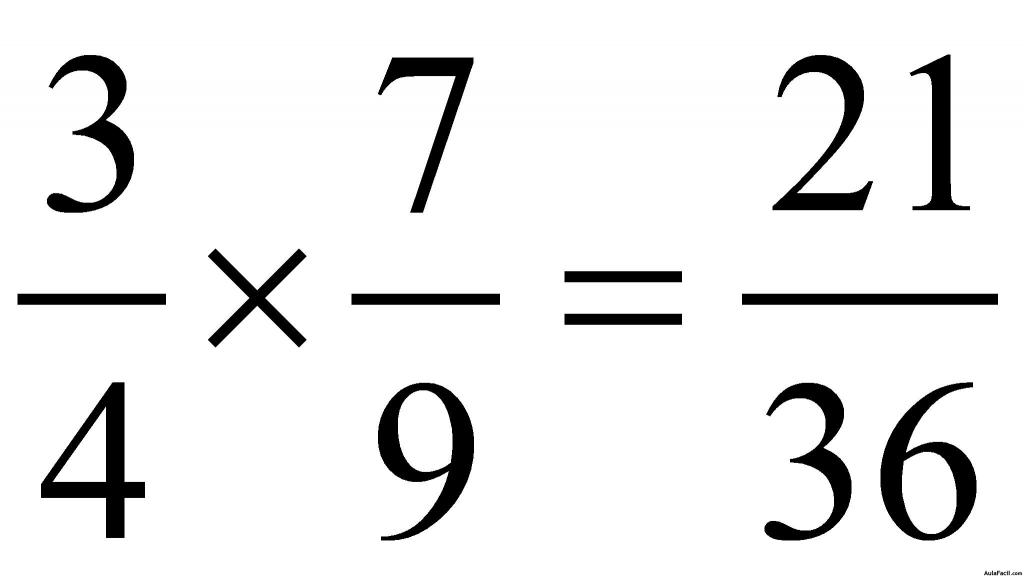
6.-Dividir fracciones:

Al dividir dos fracciones se obtiene otra fracción:

• Su numerador es el producto del numerador de la primera por el denominador de la segunda.
• Su denominador es el producto del denominador de la primera por el numerador de la segunda.

OJO!!: Para dividir fracciones utilizamos el producto cruzado.

TEMA 4: FRACCIONES

TEMA 4: FRACCIONES
1.-Fracciones:
-Concepto y términos (Numerador/denominador)
-Tipos: fracción Propia (<1), fracción Impropia (> 1), fracción Mixta (nº entero y parte decimal o fraccionaria).
2.-Fracciones equivalentes
3.-Reducir a común denominador.Comparar fracciones.
4.-Sumar y restar fracciones.
5.-Multiplicar fracciones.
6.-Dividir fracciones.

Ahora comenzamos un tema nuevo y para ello veremos este video que nos hará "reflexionar y debatir" sobre las fracciones y su significado en la vida real. "Todos somos una parte de un todo"
Estad atentos!!!.

A veces necesitamos expresar cantidades que son menores que la unidad.Seguramente habrás oído expresiones como un cuarto de kilo, medio depósito, un tercio de la población, medio litro de leche..
Es habitual encontrarnos rodeados de fracciones al hacer referencia a partes de la unidad, es decir, para expresar "trozos" de algo.
¿Sabías que una misma parte de algo se puede expresar de diferentes maneras?Por ejemplo, podemos decir que tenemos medio litro de leche o dos cuartos de litro. Ambas fracciones representan la misma cantidad si se refieren a la misma unidad. Las fracciones que representan la misma parte de la unidad reciben el nombre de fracciones equivalentes.

Para saber más!!!!
Curiosidad!!!: a las fracciones se les llamaba "QUEBRADOS", el nombre de fracción se debe a Juan de Luna, que tradujo al latín, en el siglo XII, el libro de aritmética del árabe Al Juarizmi.Este empleó la palabra fractio para traducir la palabra árabe al-Kasr, que significa "quebrar, romper". Por eso las fracciones se conocen con el nombre de quebrados.Las fracciones resultaban tan importantes para el comercio que los babilonios y los romanos utilizaban símbolos y palabras para representarlas. Los egipcios desarrollaron otro método para escribir fracciones.
Hacia el 628 d.C. los hindúes ya escribían fracciones como hoy lo hacemos, pero sin la barra horizontal.
El matemático Fibonacci (Leonardo de Pisa, s. XIII) fue el primer europeo que escribió las fracciones de la manera en que las escribimos actualmente. También a él se debe la "sucesión de Fibonacci"
(La sucesión comienza con los números 0 y 1, y a partir de estos, «cada término es la suma de los dos anteriores», 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377......).Tiene numerosas aplicaciones en ciencias de la computación, matemáticas y teoría de juegos. También aparece en configuraciones biológicas, como por ejemplo en las ramas de los árboles, en la disposición de las hojas en el tallo, en la flora de la alcachofa y en el arreglo de un cono.

Titulo: Las fracciones
Términos: fracción, numerador, denominador, equivalentes, irreducible, m.c.m., m.c.d.

6.1.- Las fracciones y sus términos. Representación.
La fracción es un número que representa una o varias partes de la unidad.

Si dividimos un objeto o unidad  en varias partes iguales, a cada  una de ellas, o a un grupo de esas partes, se las denomina  fracción. Las fracciones están  formadas por dos números: el numerador y el denominador.

Prueba escrita Tema Potencias (T3)

Finalmente, y tras acuerdo en los grupos d clase, la prueba escrita del tema 3 de Potencias y raíces será el viernes 23 de noviembre para 6ºB y 6ºC
Contenidos
Potencias
Potencias de base 10.Descomposición polinómica.
Descomposición en producto de factores primos
Aplicación de potencias al cálculo de m.cm. m.c.d.
Raíces exactas y raíces enteras (aproximación).

Tema 3 Potencias y raíces

Comenzamos tema 3 en la segunda semana del mes de noviembre.
Guión de la unidad es el siguiente:
1.-Potencias
2.-Potencias de base 10.
3.-Descomposición en factores primos ( igual q en el T2).
4.-Aplicación de Potencias al cálculo del m.c.m y el m.c.d.
5.-Raíces.Tipos: exactas y enteras

1.-Potencias: un producto de factores iguales se puede escribir en forma de potencias.
    16= 8x2= 4x2x2= 2x2x2x2


2.-Potencias de base 10: una potencia de base 10 es igual a la unidad (1) seguida de tantos ceros (0) como indica el exponente. Para escribir números con varios ceros se utilizan las potencias  de base 10. 
 Cualquier número se puede escribir como suma de sus cifras multiplicadas por potencias de base 10.

3.-Descomposición en factores primos.
      12= 4x3= 2x2x3
      12 = 3 × 22

Realizar la descomposición en factores primos o descomposición factorial de un número es escribirlo como producto de números primos.

4.- Aplicación de potencias al cálculo del m.c.m. y el m.c.d.

El m.c.d. de dos números es el producto de los factores primos comunes elevados al menor exponente. Si no tienen ningún factor en común el m.c.d. de los números es 1.
         8 = 23       12 =22 × 3.                  m.c.d. (8, 12 ) = 22 = 4

El m.c.m. es el producto de todos los factores primos elevados al mayor exponente.
         8 = 23          12 =22 × 3.             m.c.m. (8, 12) = 23 x 3 = 24


La prueba escrita de este tema: será en la última semana del mes de noviembre. Entre el 22 y 29 de noviembre.